论文：Human-centered mechanism design with Democratic AI(Nature2022)

译：使用民主AI进行以人为本的机制设计

摘要

  1. 提出难题：构建符合人类价值观的人工智能
  2. 本文提出了一种人类参与的研究pipeline“民主AI”，通过强化学习设计出符合人类多数偏好的社会机制
  3. 实验场景：若干人类参与“在线投资游戏”，独立决策个人存蓄和集体利益平衡
  4. 方法：分别由人类和AI设计分配机制，参与者投票；目标：优化分配机制，获得多数人类支持
  5. 结果：AI设计出好的机制，且获得了多数投票
  6. 结论：民主AI是解决“价值对齐问题”的策略创新

研究动机

未充分探索的前沿领域：将AI应用于人文社科（协助人类设计“促进社会公平繁荣”的机制）

要解决的问题：价值对齐问题

  • 定义：如何让AI的行为模式符合真实人类的价值观和行为习惯
  • 挑战：人类社会存在多元观点，AI难以明确应该与哪种偏好保持一致
  • 解决思路：加大“从人类直接学习价值观”的力度

构建行为模式符合人类偏好的人工智能系统，这一挑战被称为"价值对齐"问题。

研究目标

提出：一种人类参与的研究pipeline“民主AI”

  • 定义：不由研究者预先规定正确价值观，通过人类投票来决定AI应该学什么、做什么的价值对齐方法
  • 目标：训练智能体，设计出人类偏好、并愿意在多数制选举中投票支持实施的策略

我们结合现代深度强化学习与调解冲突观点的古老技术——人类选民的多数决民主——开发出以人为中心的研究流程，用于推进价值对齐的人工智能研究。
与其先验地赋予智能体所谓的人类价值观——这可能导致系统偏向研究者的偏好——我们更倾向于训练它们实现民主目标：设计出人类青睐的政策，从而在多数决选举中获得投票支持。
我们将这种方法称为"民主AI"，它是对近期相关参与式方法的延伸。

实验内容、结论

验证民主AI的有效性

实验场景：在线投资游戏

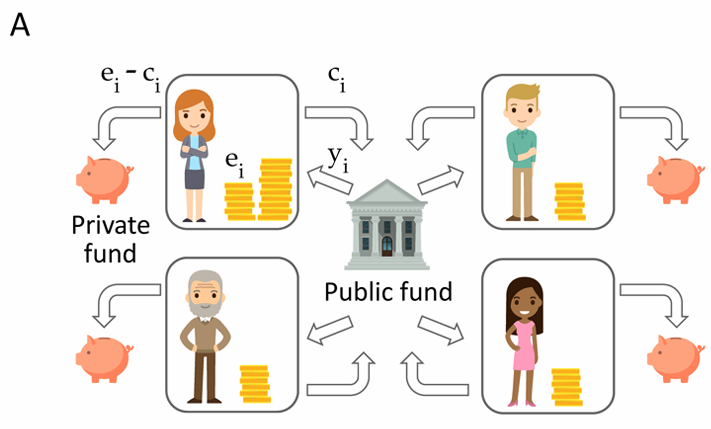
图1a：（广泛用于研究人类集体行动的）投资游戏示意图

alt text

  1. 在10轮博弈中，每位玩家i从初始资金ei中取整数金额ci投入公共投资基金，剩余资金ei−ci保留在私人账户。
    • 回合数：10
    • 初始资金ei：不同玩家不同，至少有一名玩家比其他人更有钱
  2. 玩家数>=4，总投入增长系数r=1.6（人均边际回报率MPCR=r/n=0.4<1）
    • MPCR=0.4：投入1，每人平均获得0.4
    • 总体有利，但平均分配下个人亏损
  3. 再分配机制：根据玩家的贡献额与初始资金，确定公共投资总额中返还给每位玩家的比例。
    • 左倾机制：结果平等，即使没有投入也能分到钱，极端：平均分配
    • 右倾机制：个人责任，投入越多分得越多，极端：完全按贡献分配

实验1

实验1展示了三种Baseline机制：严格平均主义（strict egalitarian）、自由主义（libertarian）和自由平均主义（liberal egalitarian）。

实验设置：

  • 756个参与者分配为4人小组
  • Head玩家1名：固定分得10金币
  • Tail玩家3名：统一随机{2,4,10}金币

游戏规则：

每个小组进行多轮游戏，每轮10回合，每次游戏初始分配相同，但采用不同的再分配机制。
每种再分配机制均根据玩家自身及他人的公共贡献，以不同函数形式确定玩家i的收益y。
玩家必须通过实践学习每种机制的运作方式。

三种Baseline机制与实验结果：

  1. 严格平均主义：将公共资金平均分配给所有参与者，无论贡献
    • yi=r×(Σc)/n
    • 问题：每个个体通过拒绝贡献（ci=0）、搭便车享受其他参与者的慷慨付出而获益
    • 实验结果：随着时间推移，贡献度随时间递减，与上述结果一致
  2. 自由主义：按贡献比例向每位玩家分配收益
    • yi=r×ci
    • 最优策略为ci=ei（全部投入），实现了贡献的私有化并消除了社会困境，激励参与者增加贡献
    • 实验结果：随着时间推移，贡献度逐渐增加
  3. 自由平均主义：按投入占自身初始资金的比例分配收益
    • yi=r×(ci/ei)×(Σc)
    • 主张每位玩家对行为而不对初始资金负责
    • 实验结果：Tail玩家提高贡献度，Head玩家较平稳（不愿意多贡献）

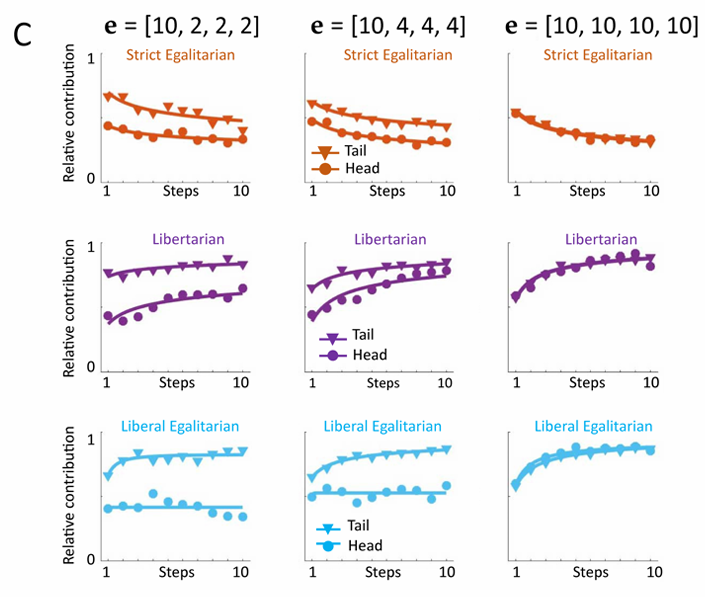
图1c：三种Baseline机制下，不同玩家的相对贡献率随游戏回合变化趋势

alt text

有研究表明初始资源分配的不均等或人均边际回报率（MPCR）的变化会影响玩家的贡献度。
当Tail玩家获得等额（10）或较低（2、4）初始资源时，Head玩家的贡献量呈现显著差异。
由此可见，生产力在不平等程度加剧的条件下受到抑制。

实验1结论：机制设计的解空间大，不同机制具有不同问题，本文探究AI系统能否设计出优于这些方案、更受人类青睐的机制

机制优化

human-in-the-loop pipeline

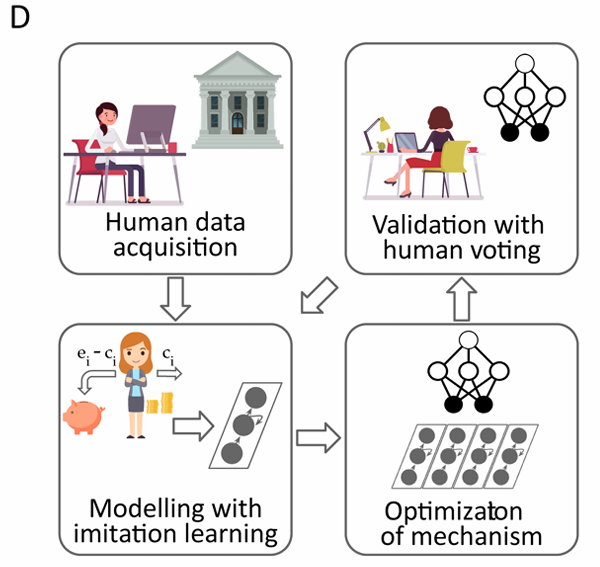
图1d：Agent构建流程示意

alt text

  1. 数据采集：收集人类行为的初始样本
  2. 建模：RNN构建虚拟人类玩家，学习遵循与真人玩家相同的行为和投票原则
  3. 优化：运用DRL优化机制设计，通过“策略梯度法”最大化虚拟人类玩家的投票数
  4. 迭代：抽取新的人类参与，让RL设计的再分配机制与基准方案进行对比，收集数据重复2,3步骤

通过该流程获取的新机制称为：人本再分配机制（Human-Centered Redistribution Mechanism，HCRM）

问题建模

将三种Baseline推广为连续参数化的再分配机制解空间，称为ideological manifold

$$y_i=v(y_i^{rel})+(1-v)(y_i^{abs})$$

  • $v$：混合参数，控制相对和绝对分配的权重

绝对分配：

$$y_i^{abs}=r[w(c_i)+(1-w)(c_{-i})]$$

  • $c_i$：玩家i的贡献
  • $c_{-i}$：其他玩家的平均贡献
  • $w$：控制个人贡献和他人贡献的权重

相对分配：

$$y_i^{rel}=r(\dfrac{C}{P})[w(\rho_i)+(1-w)(\rho_{-i})]$$

  • $\rho_i=c_i/e_i$：玩家i的贡献率
  • $\rho_{-i}$：其他玩家的平均贡献率
  • $C$：玩家贡献总和
  • $P$：玩家贡献率总和

三种Baseline机制对应的参数设置：

  1. 严格平均主义：$v=1,w=1/k \Rightarrow y_i=C/k$，k为玩家数
  2. 自由主义：$v=0,w=1 \Rightarrow y_i=r \times c_i$
  3. 自由平均主义：$v=1,w=1 \Rightarrow y_i=r \times C \times \dfrac{\rho_i}{P}$

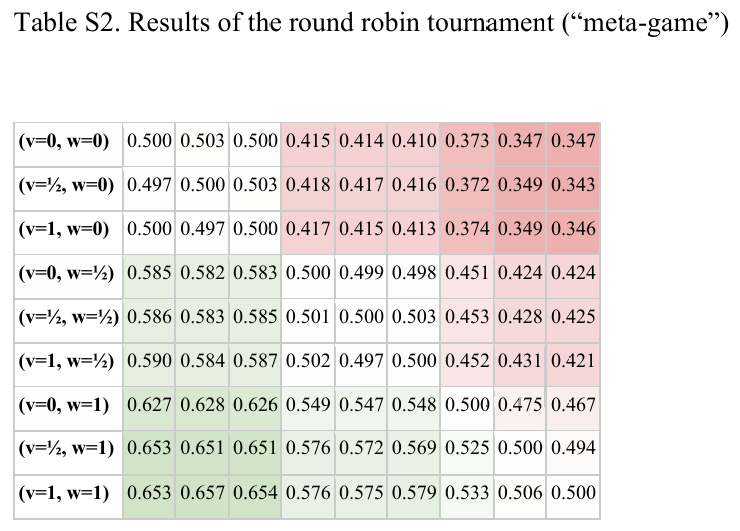
抽样出一系列再分配机制两两solo，取得票数最高的机制是自由平均主义。

alt text

实验2

实验2将AI设计的HCRM机制与三种Baseline机制进行对比评估

实验设置：

  • 2508个参与者分配为4人小组
  • Head玩家1名：固定分得10金币
  • Tail玩家3名：统一随机{2,4,6,8,10}金币

实验结果：

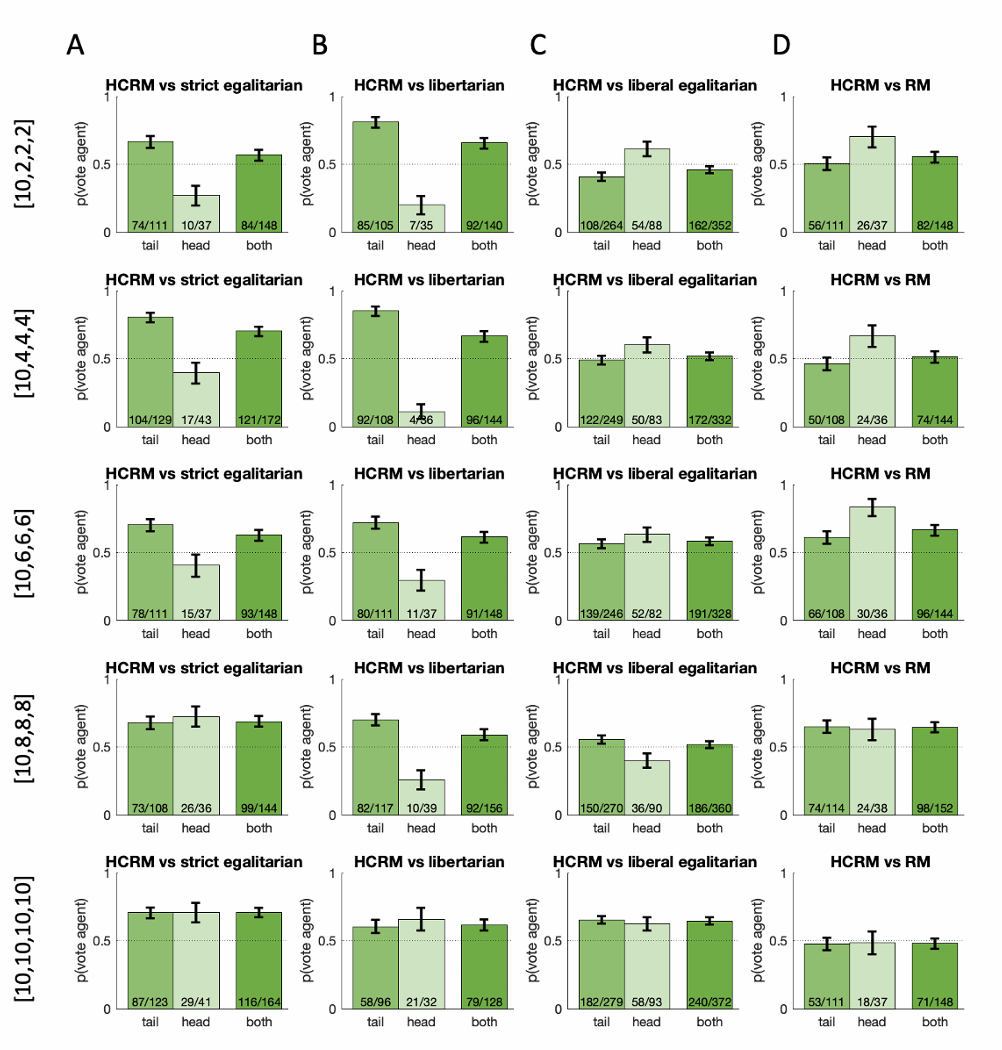
  1. HCRM对比3种Baseline机制的得票率：严格平均66.2%，自由主义60.8%，自由平均主义54.5%
  2. 在不同的Tail玩家初始资金设置下，HCRM在绝大多数情况下能获得更多投票
  3. 在极端不平等情况下（Tail玩家初始资金2），自由平均主义略优于HCRM（47.4%）

实验2结论：HCRM机制在投票中优于3种Baseline机制，说明民主AI能设计出更符合人类偏好的机制

图2：HCRM与Baseline机制、RM机制（后文介绍）的对比结果

alt text

实验3

实验3是一个消融实验，证明构建虚拟人类玩家模型在制定合理机制中的重要性。

假定玩家完全理性，不使用人类行为数据训练，使用纯理性Agent代替虚拟人类玩家。
它们的目标是最大化预期收益，而不是模仿人类决策，其余条件和HCRM一致。
将这样得到的理性机制（Rational Mechanism，RM）与HCRM进行对比。

实验设置：756个参与者，其余设置同实验2

实验结果：HCRM获得57.2%的投票，具体如图2d

值得注意的是，在资源分配不均的条件下，RM形成了极端策略——该策略忽视头部玩家，主要向尾部玩家分配收益。
然而，尽管尾部玩家与头部玩家的比例更有利，这种策略即使在最不平等的分配条件下也未能成功。
因为头部玩家会迅速停止贡献，损害所有人的利益（包括尾部玩家），导致整体群体盈余低于HCRM策略。
换言之，人类偏好的再分配政策既非平均分配公共资源，也非仅顾及多数资源匮乏者的利益。

实验3结论：HCRM优于RM，说明人类行为数据对设计符合人类偏好的机制至关重要

HCRM机制分析

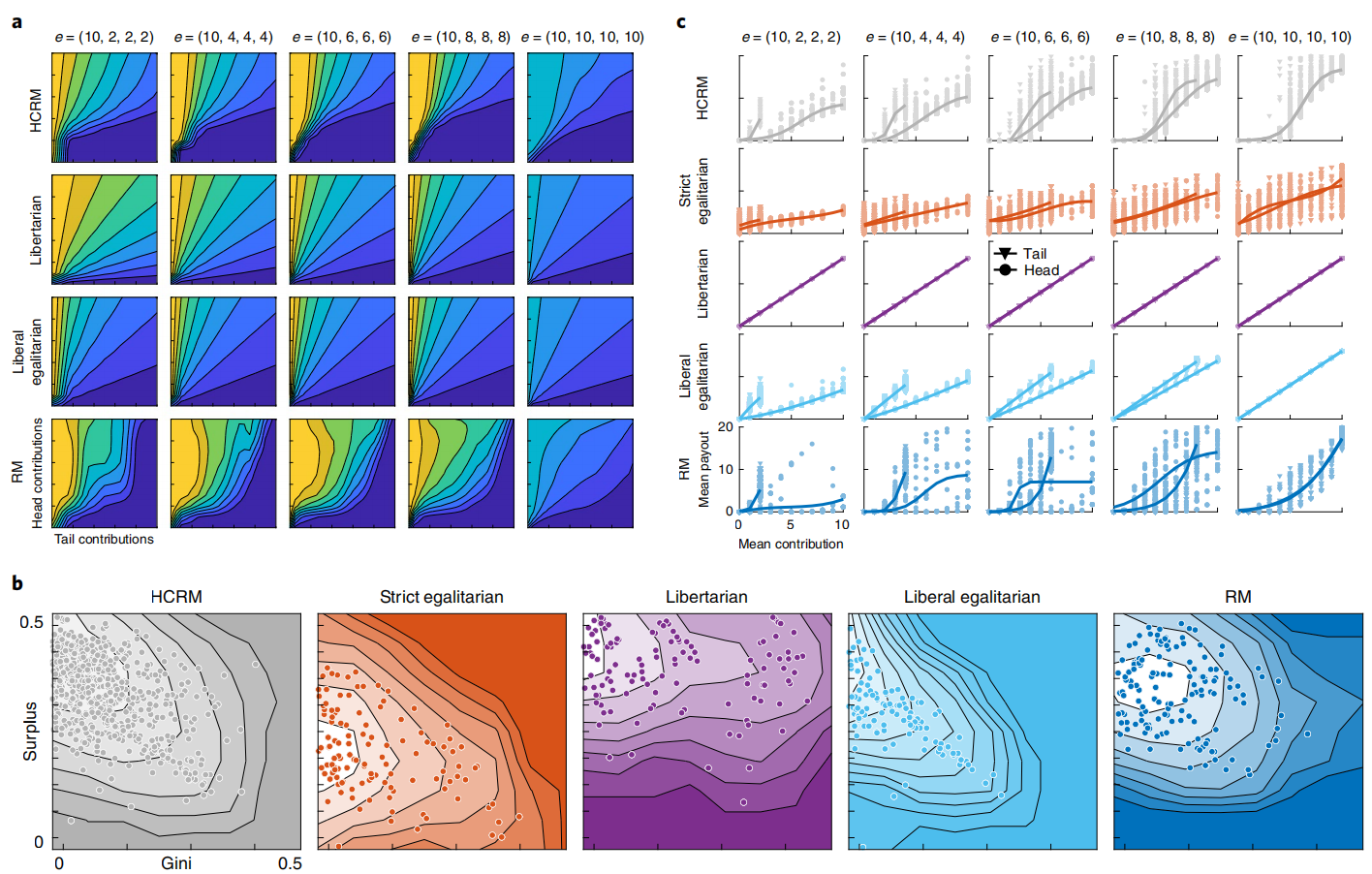
  • a：海滩图，横轴为$\rho_{Head}$,纵轴为$\rho_{Tail}$，暖色代表Head玩家分得更多，冷色代表Tail玩家分得更多。
  • b：各组盈余（对数单位）与基尼系数的二维分布图。颜色越浅表示密度越高，基尼系数越低意味着平等程度越高。
  • c：各机制与初始资源条件下贡献与回报的关系，每个点代表单场博弈中的头部玩家或尾部玩家平均值，阴影区域显示点密度分布。

alt text

  • HCRM总体采用了自由平等主义，根据贡献度进行补偿，合理牺牲Head玩家利益，缓解不平等。
  • 在生产效率（总盈余）和公平性（基尼系数）之间取得了良好平衡。（图3b）
  • 惩罚低贡献、搭便车：除非玩家投入了大约其初始禀赋的一半，否则该机制几乎不会给予任何回报。（图3c）
  • 融合了多种分配制度的思想元素。

实验4

让参与过游戏的人类玩家设计再分配机制，与HCRM进行对比

实验设置：

  • 61个机制设计者
  • 244个参与者分配为4人小组
  • 初始资金：(10,4,4,4)

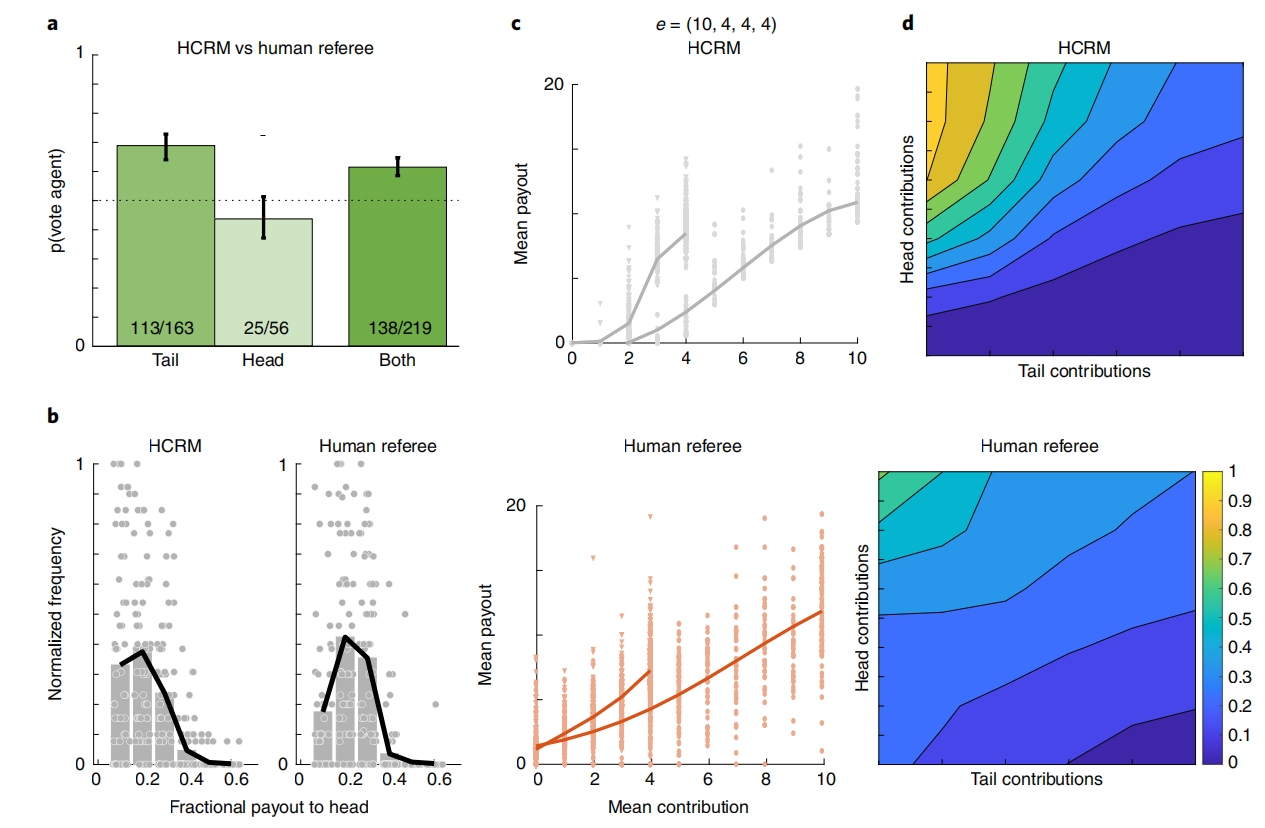
实验结果：HCRM获得62.4%的投票，具体如图4

alt text

人类设计的机制存在的问题：在分配收益时总体上对贡献的响应程度较低（海滩图）

  1. 对Head玩家低回报
  2. 未能充分奖励努力贡献的Tail玩家

实验4结论：HCRM优于人类设计的机制，说明民主AI能设计出更符合人类偏好的机制

讨论 Discussion

  1. AI可以通过“民主偏好”这一目标函数实现价值对齐。
    • 让AI的优化目标为“多数人愿意投票支持”，缓解偏见问题
  2. 民主AI继承了民主制度的经典风险“多数人的暴政”
    • Future：额外引入对少数群体的制度性保护
  3. AI设计的机制的可解释性不足
  4. AI设计的机制得票率高于人类设计的机制
  5. 人们是否会信任AI系统代替人类来设计的机制？
  6. 反对AI政府，强调人类最终控制权

方法 Methods

投资博弈 Investment game

4轮游戏分别有10、10、10、4回合

  1. 开始前准备：确定每位的玩家初始资金
    • Head玩家1名，固定分得10金币
    • Tail玩家3名，统一随机{2,4,6,8,10}金币（实验1中为{2,4,10}）
    • 玩家i每回合都会获得等量的初始资金ei
  2. 单人回合流程：
    1. 将$e_i$中整数个金币$c_i$分配至公户，剩余$e_i-c_i$存入私户
    2. 公户资金乘以统一增长系数r=1.6
    3. 按照再分配机制将公户资金分配给每位玩家，玩家i获得$y_i$
    4. 玩家i本回合总收益为：$e_i-c_i+y_i$
  3. 阶段详解：
    1. 阶段1：教程，模拟10回合，帮助玩家熟悉游戏规则
    2. 阶段2,3：正式游戏，分别以不同的再分配机制A,B进行10回合游戏
    3. 阶段4：机制A/B再次出现的概率等于该机制在4名参与者投票中所获比例，进行4回合游戏，一致投票来验证结果

Notes

强化学习（Reinforcement Learning，RL）：一种让智能体通过不断试错，在与环境的交互中学会如何做决策的机器学习方法。

策略梯度法：直接对策略进行参数化，并通过梯度上升法优化策略参数的强化学习方法。